
Negras juegan y hacen tablas
Me crucé con una explicación en el canal de Suren de este precioso y famoso problema de ajedrez de Gioachino Greco, que data de 1623. Se considera a Greco –apodado «el calabrés»– el primer jugador profesional de ajedrez. Son muy famosas sus partidas contra oponentes anónimos («NN») que probablemente inventaba para plantear algunos problemas y sus soluciones.
En este problema es el turno de las negras y deben hacer tablas. Están en inferioridad, con dos peones menos. A simple vista parece probable que en esta posición las blancas puedan avanzar sus peones poco a poco hasta acabar coronando y ganando la partida. Así lo cree también Stockfish –uno de los más potentes motores de análisis de ajedrez– cuando se le alimenta esa posición.
La posición en notación FEN es:
r7/8/8/5bk1/8/5B2/5RPP/6K1 b - - 0 1
La primera opción para las negras es lógicamente 1… Ra1+ salvando la torre amenazada y dando jaque. Las blancas intentarán cambiar piezas para llegar con los dos peones a un final con superiodidad, de modo que responden interponiendo la torre, 2. Rf1.
Hasta aquí todo el mundo –humanos y máquinas– están de acuerdo y la evaluación del motor de Stockfish marca +2,4 para las blancas con profundidad de evaluación 38 (todos los posibles 19 movimientos completos por bando).
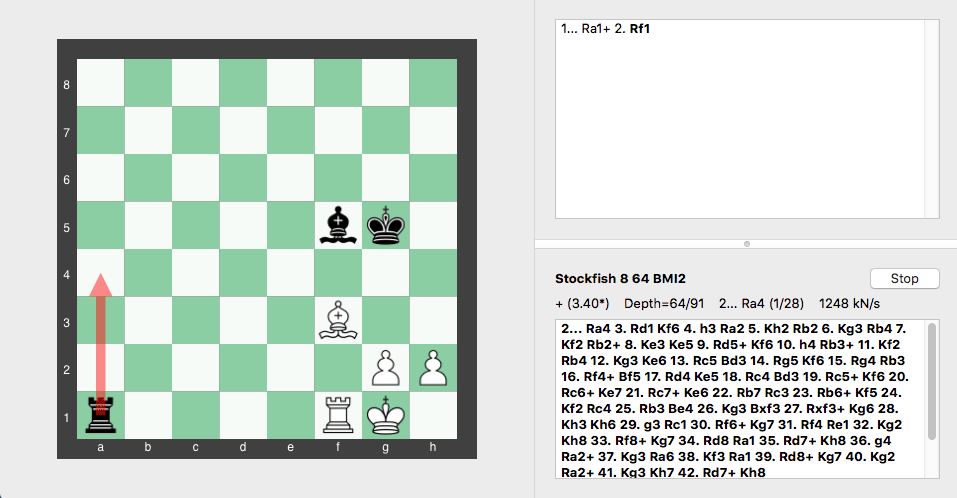
La recomendación errónea en la que se obceca Stockfish para intentar salvar la situación…
… habiendo examinado los siguientes 32 movimientos posibles de cada bando y todas sus respuestas
Lo divertido viene ahora, en el turno de las negras. Las máquinas recomiendan 2… Ra4 escapando con la torre a una fila estratégica. Pero ese no es el movimiento ganador para que las negras fuercen las tablas. De hecho si se juega la partida se vuelve en un aburrido baile de ataque y defensa muy técnico hasta que inexorablemente las blancas coronan uno de los peones en dama, cambian la dama por la torre y fin.
¿Puedes encontrar la solución?
.
.
.
El movimiento que resuelve el problema es 2… Rxf1, capturando la torre. Es demasiado duro para las negras hacer esto, pero es el camino. Es repelente porque equivale a usar la estrategia que parece ir mejor a las blancas (cambiar piezas). Y al hacerlo, la máquina sigue diciendo que las blancas están mejor.
La continuación sigue lógicamente con 3. Kxf1 y luego otro gran movimiento: las negras vuelven a hacer otro sacrificio aparentemente suicida: 3… Bh3. Las blancas capturan entonces con 4. gxh3 y la partida es técnicamente tablas. Pero la máquina sigue evaluando que las blancas están mejor.
¿Por qué es tablas? El alfil blanco ataca las casillas blancas y las casillas de llegada de ambos peones son negras, de modo que como saben quienes han estudiado un poco es un final teórico de tablas, que se puede defender con relativa facilidad. (El alfil está obligado a defender el peón y si el rey blanco se acerca el negro se pueden forzar tablas por rey ahogado o incluso capturar el peón).
Lo increíble es que a día de hoy los ordenadores no superen esta situación para un problema que tiene más de 400 años (!) y que motores tan potentes como Stockfish no analicen correctamente el final, en el que incluso dan +6,5 puntos de ventaja a las blancas al sumar el valor del alfil, los peones y la «mejor posición». Sencillamente no pueden ver el final porque está más allá del horizonte al que pueden llegar con su análisis.
Quizá con ordenadores más potentes ese análisis sea posible, o bien enseñándoles ciertas reglas sobre situaciones peculiares como las de este problema. Otra posible solución sería el uso de bases de datos de tablas de finales, que existen al completo hasta 7 piezas (aunque muy grandes y pesadas: por lo que vi este final está en la Scorpio 6men de las Syzygy tables @ OICS Chess and EGTB Tracker, pero no llegué a descargarla).
En mi exploración del problema tuve que forzar a jugar a la máquina contra sí misma durante 84 jugadas más para convencerla, hasta que el bando blanco acabó desesperadamente dejándose capturar ambos peones para finalmente declarar

… «es tablas».
Relacionado,
- Otro problema de ajedrez capaz de «derrotar» a los ordenadores
- Matemáticas y ajedrez, máquinas y algoritmos analizan sobre el tablero
- El reto de las damas de ajedrez y el millón de dólares
- Estudios sobre aprendizaje automático en las damas (allá por 1959)
- Juegan blancas y mate en 549
- El ajedrez de la Thinking Machine 6 permite ver qué se está calculando
- Hordas vs. hordas en ajedrez poco convencional


