Por @Alvy — 12 de Agosto de 2011
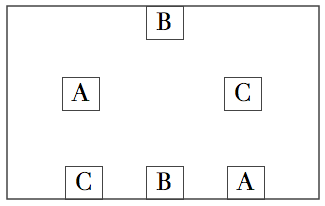
Este es el típico problema en el que hay que conectar las cajas con líneas que no se crucen, es decir: de la A a la A, de B-B y de C-C. No hay trucos raros; la cuestión principal tiene solo dos posibles respuestas posibles: sí o no.
¿Es posible resolver el problema?
Demuéstralo
Este problema inventado por Denise Hunter proviene de la edición en papel de Why Not? de Barry Nalebuff y Ian Ayres, un libro muy recomendable sobre cómo resolver problemas de todo tipo, tanto de los cotidianos como puzzles, acertijos y otras cuestiones interesantes.
