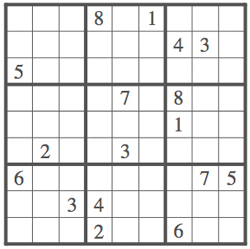
Los sudokus buenos, buenos, de pata negra fetén, tienen una solución única sergún la definición más estricta de este pasatiempo matemático. Desde hace tiempo se especulaba con cuál sería el sudoku mínimo, es decir, cuántos «números-pista» iniciales debía tener como mínimo un sudoku para que su solución fuera única.
Unos matemáticos publicaron recientemente un trabajo donde analizaban el problema. Puede leerse al completo en There is no 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem. La conclusión es que, como se suponía y ellos han podido demostrar, hacen falta como mínimo 17 números iniciales para componer un sudoku de solución única.
Para llegar a la solución examinaron mediante software y fuerza bruta unos 5.500 sudokus seleccionados a partir de ciertas premisas, demostrando básicamente que no había sudokus de 16 números con soluciones únicas. Así que como con 17 números iniciales sí que se conocen muchos, ese es el valor buscado.
Hay algo más de información sobre el tema en Gaussianos: Demostrado: un Sudoku debe comenzar con 17 números dados para que pueda tener solución única.