Esto sí que me ha sorprendido: Cory Doctorow cuenta en Boing Boing que los números suelen comenzar más frecuentemente por «1» que por cualquier otro dígito. Así como suena.
Una teoría matemática llamada Ley de Benford predice que en un conjunto determinado de números, aquellos cuyos primer dígito es «1» aparecerán de forma más frecuente que los números que empiezan por otros dígitos. Benford, un físico de General Electric formuló esta ley en 1938, tras descubrir que un libro de tablas de logaritmos de GE había bastantes más páginas dedicadas a los números que empezaban por «1» que a los demás. Como los números que empiezan por «1» aparecen tan a menudo, es posible descubrir a tramposillos (con los impuestos, con los deberes de clase, etc.) simplemente comprobando si los números que se inventan tienen esa desviación hacia los que comienzan por «1» más frecuentemente que los otros, o no. Este sistema no es perfecto, claro - en un artículo de 1998 el New York Times explicaba que gente que tiene dietas de 25 dólares para cenar a veces pasaba tickets de 24,90... pero aun así es fascinante.
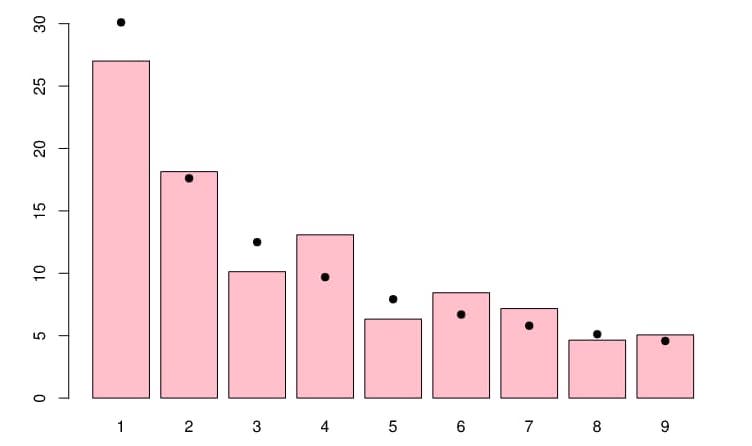
Como dice Cory, la ley de Benford es realmente fascinante. Benford trabajó con más de 20.000 conjuntos de números de todo tipo: longitudes de ríos, estadísticas de beisbol, números de las calles de cientos de personas, hasta poder tener datos suficientes para enunciar su teoría. Como se ve en el gráfico del artículo, la frecuencia esperada para números que comienzan por 1 es casi del 30%, para el 2 es de un poco más del 17%, para el 3 algo más del 12% y para el resto disminuye. Los conjuntos en los que sucede esto muestran invariancia de escala: si se trata de un conjunto como valores de la bolsa o de divisas, da igual si se usan tablas en yenes o dólares o euros, por ejemplo.
Como apunta Cory, el artículo original del New York Times contiene algunos errores matemáticos obvios (en el cuadro de ejemplos), pero aun así es una buena explicación.
Buscando por ahí encontré Benford's Law en MarthWorld, uno de mis sitios de referencia favoritos, mucho más tecnico y a la vez preciso. Allí se explica esta ley fenomenológica con muchos más ejemplos asombrosos. El más fácil de comprobar es tal vez utilizar una base de datos de direcciones con números de calles (el 30 por ciento más o menos deben empezar por «1»). La fórmula, cuando es aplicable a un conjunto de datos, es algo así como:
La probabilidad de que el primer dígito de X sea n es aproximadamente
Log10(n+1) - Log10(n)
Al parecer este fenómeno tiene que ver con cómo los seres humanos usamos los números en la práctica a partir de conjuntos procedentes de la la naturaleza (o el MundoReal™). No fue hasta 1996 que un matemático llamado Ted Hill dio con una demostracion matemática de lo enunciado por Frank Benford en 1938, a pesar de que la ley resultaba obvia con sólo hacer algunas comprobaciones sencillas - siempre que el conjunto de datos fuera válido, porque no todos lo son. La demostración tiene que ver con algunos teoremas del límite central y su relación con el comportamiento de las mantisas en las multiplicaciones de valores aleatorias.
En la Wikipedia en inglés, la Ley de Benford está incluso mejor explicada (también en español: Ley de Benford). Si un conjunto de números «del MundoReal™» tiene cierta distribución, ésta debe ser invariante a la escala (es decir, deben estar distribuidos igual ya midas algo en metros o yardas o lo que sea). Por ejemplo un valor que no empiece por cero, como «1 metro coma algo» puede equivaler a 3, 4 ó 5 pies. Si se estudian todas las conversiones entre posibles escalas se observa que hay una distribución logarítimica, que es precisamente la Ley de Benford. En algunos casos (las distribuciones «normales», como las alturas de la gente o los CI) la ley no es aplicable, aunque «reaparece» de repente si se recombinan con otros valores de forma aleatoria - esto es doblemente curioso.
Como dice el artículo original, antes de que empieces a pensar que la Ley de Benford te podría servir para predecir los números de la Loto, recuerda que no es el caso: a diferencia de los números «reales» seleccionados por seres humanos o por la naturaleza, los números de los bombos son sólo una «representación» de números. En los sorteos aleatorios, la distribución es del tipo «normal» y no se observan los resultados de esta Ley. Bueno, siempre puedes comprobar las tablas si no te fías, como hizo Benford...
(Vía Boing Boing.)
Actualización: Un interesante enlace que también llegó a Boing Boing como demostración visual: Significant Figure Distribution Generator, que muestra cómo resulta la distibución de «primeros dígitos» cuando eliges cualquier número y un factor mutiplicador, y vas haciendo las multiplicaciones y fijándote sólo ese primer dígito.
Actualización: Hoy comprobé las frecuencias de los primeros dígitos de una lista de la compra (en euros), una lista con 52 elementos, con este resultado: «1» 47%, «2» 23%, «3» 17%, «4» 5%, «5» 7%, «6» 1%, «7», 1%, «8» y «9», 0%. Encaja bastante bien y eso que no eran demasiados elementos. Se supone que si haces la conversión a pesetas o dólares sucedería lo mismo, pero no me aparece tecleármela entera ;-)


