La escalera infinita es una escalera que se construye comenzando por un cuadrado y añadiendo escalones cada vez más pequeños. Cuando el proceso se repite y se lleva al infinito produce una aparente paradoja: la diagonal del cuadrado parece tener dos valores distintos a la vez. Lo explica Henry Segerman para Numberphile como bonus con truqui para su explicación sobre las curvas que rellenan el plano y el espacio, con lo que está relacionado.
Si el cuadrado tiene lado 1 sabemos que su diagonal mide √2 (por el teorema de Pitágoras). En el primer paso de la construcción de los escalones se ajustan a la mitad de cada lado: los primeros tienen 1/2 de alto y 1/2 de fondo; como hay 4 segmentos su longitud son 2 unidades. En la siguiente división tienen 1/4 y 1/4, son 8 y también suman 2 unidades. Luego 1/8 y 1/8, sumando también 2, etcétera.
En este dibujo de Too Damn Logical puede verse bastante claro:
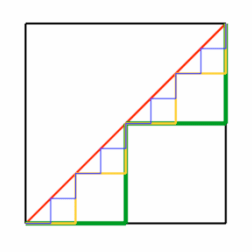
Negro - cuadrado original / Rojo - diagonal
Verde - paso 1; Amarillo - paso 2; Azul - paso 3
El problema surge cuando se repite la operación hasta el infinito. El infinito hace cosas muy raras y es bastante peligroso de utilizar en demostraciones si no se tiene en cuenta cómo debe aplicarse exactamente. Aquí, por ejemplo, si se da por supuesto (como sería bastante obvio e intuitivo, por otro lado) que una escalera infinita de escalones infinitamente pequeños tendría el mismo aspecto y sería igual que la diagonal, cosa que no es, la longitud de la diagonal valdría 2 unidades (!) pero cuando sabemos que en realidad vale √2 (1,4142…)
¿Qué ha sucedido? El razonamiento cae en una de esas trampas del infinito. En Quora lo explican con todo lujo de detalles pero básicamente se debe a suponer que la función que lleva cada curva a su longitud es una función continua. Otra forma de verlo es que las funciones que dibujan la diagonal y las escaleras son distintas; en realidad las escaleras solo tocan la diagonal en ciertos puntos (y aparentemente una mayor parte queda fuera sin tocarla). Si se emplea cálculo diferencial con esas funciones, la de la diagonal y la de la escalera, se puede obtener √2 para la diagonal y 2 para la escalera sin mayor problema.
Relacionado:


