Cuestión fractal

Por @Alvy — 12 de Septiembre de 2009

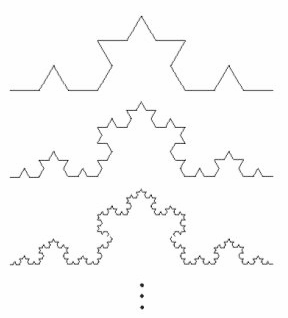
Koch-Fractal

Cuestión: ¿Cuánto mide la costa de Inglaterra?
— Microsiervos (@microsiervos) December 18, 2015

Nota: La encuesta original tenía tres opciones (1) 12 500 Km (2) Depende del tamaño de la regla con que la midas y (3) Infinito. Pero se perdieron todos los datos y ha habido que recrearla en Twitter. (Dejando dos opciones)

Un libro de @Alvy y @Wicho

Se suponía que esto era el futuro
Ciencia, tecnología y mucho más
www.microsiervos.com/libro