Por @Alvy — 29 de abril de 2010
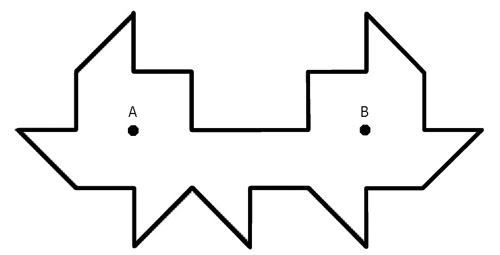
Si esto fuera un hoyo de mini-golf «teórico», y la pelota se moviera siempre en línea recta, rebotando de forma perfecta e ideal en las paredes, sería imposible hacer un «hoyo en uno» desde A hasta B: el campo está diseñado de tal modo que la bola rebotaría por siempre jamás sin llegar nunca a su destino. El problema original data de 1950 y fue resuelto en 1995; desde entonces se han ido mejorando las soluciones con figuras de menos lados.
Una forma interesante de ver el problema es imaginar que se trata de una habitación llena de espejos perfectos en los que se enciende una vela en el punto A. Debido a su particular diseño, la luz nunca llegaría al punto B.
(Vía Futility Closet.)
