Por @Alvy — 1 de Enero de 2012
2011 
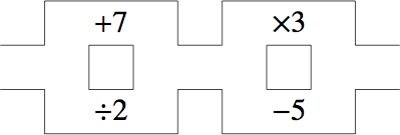2012
Hay que pasar de 2011 a 2012 siguiendo el camino y realizando las operaciones cualquier número de veces, pero no vale retroceder para repetir la misma dos veces seguidas.
(Vía Mathpuzzle.)
Los megabytes que entran por los que van saliendo
