Por @Alvy — 18 de Marzo de 2009
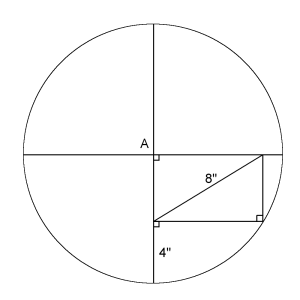
Si A es el centro, ¿cuánto vale el radio del círculo?
Futility Closed es un altamente recomendable blog que suele deleitar con curiosidades numéricas sorprendentes muy a menudo. El otro día publicaron este problema geométrico para que lo resolvieran los lectores. Lo titularon Round Numbers: consiste en averiguar el radio del círculo del dibujo.
A es el centro, los cuadraditos en las esquinas indican ángulos rectos y las medidas 8" y 4" son las longitudes de los segmentos indicados (están en pulgadas, pero en este caso las unidades no son relevantes).
Es bueno dedicarle un rato a averiguar la solución, que publicaron al día siguiente y puede leerse en la misma página.
