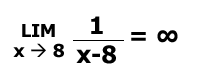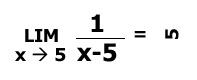Por @Wicho —
Otro ejemplo de matemáticas creativas demasiado bueno para ser cierto (traduzco del original en inglés que me llegó por correo electrónico):
Después de explicar a una estudiante mediante varias lecciones y ejemplos que(Gracias, Antonio.)
Intenté averiguar si realmente lo había entendido, así que le puse otro ejemplo.
Este fue el resultado: