Qué simpático y extraño a la vez me ha parecido el teorema de Pick que descubrí en Futility Closet. Se aplica a polígonos cuyos vértices tienen coordenadas enteras; en otras palabras, formas cerradas que puedes dibujar pasado por los «cruces» de una retícula de cuadrados como las de un cuaderno.
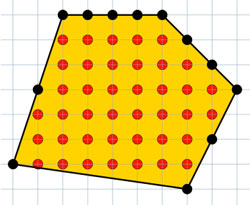
Resulta que si cuentas los puntos hay están en el interior (i) y en los que hay en intersecciones de los bordes (b), el área de la figura es exactamente A = i + (b/2) - 1. En este ejemplo hay 40 interiores y 12 en el borde, por tanto el área es A = 40 + 12/2 - 1 = 45.
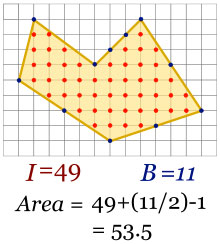
A veces el resultado no es un número entero, como en este otro ejemplo procedente de la Wikipedia, donde el área es 53,5. Cuando se desarrolla la demostración todo encaja y tiene su lógica, pero a simple vista no es trivial descomponer los polígonos en triángulos ni calcular su superficie; como atajo es sorprendentemente genial.