En este episodio del siempre recomendable canal de divulgación Numberphile nuestra admirada matemática Holly Krieger de la Universidad de Cambridge explica de forma fácil y visual lo que es la conjetura de Mertens y de dónde sale uno de los números más grandes que se conocen en una demostración matemática.
Esta conjetura es interesante porque es de ese tipo de problemas con números naturales, fáciles de entender pero de consecuencias imprevisibles: aparecen unos patrones más o menos reconocibles y donde por lo que sucede al principio se podría intuir lo que sucede al final, y que la demostración será fácil… pero no. Esta conjetura se demostró falsa casi un siglo después de ser enunciada.
El problema tiene que ver con la forma en que aparecen los factores primos de los números naturales, lo cual se puede explicar con una función: si el número tiene un número par de divisores primos (por ej. 10 = 2 × 5, tiene dos) se dice que el resultado es +1, si es impar (ej. 30 = 2 × 3 × 5, tiene tres), -1 y si cualquier factor primo se repite (ej. 8 = 2 × 2 × 2, tiene tres, pero alguno repetido), simplemente se ignora.
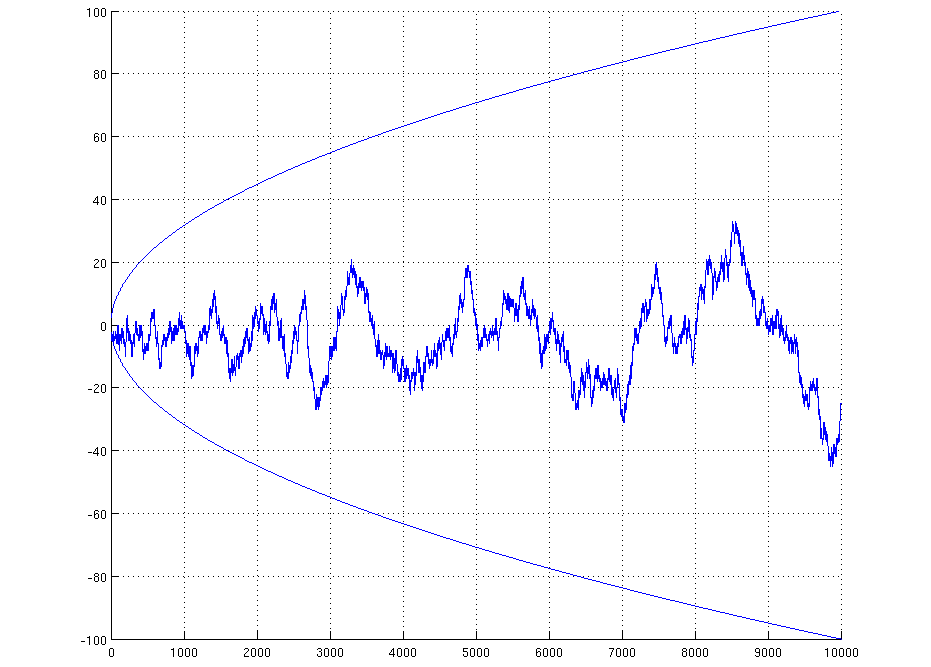
La conjetura de Mertens oscilando en sus 10.000 primeros valores alrededor del 0.
La conjetura dice que probablemente nunca se saldrá de la curva (raíz cuadrada de n) / (CC) Wikimedia
Sumando y restando todos esos resultados desde 1 hasta el número deseado se obtiene un valor, que parece oscilar alrededor del cero. Esto tiene cierto sentido porque al hacer la lista a veces se suma +1 y a veces se resta -1. La «cosa» oscila un poco más arriba o más abajo, pero no demasiado, aparentemente; una forma de visualizarlo es una gráfica estilo paseo aleatorio con el +1 hacia arriba y el -1 hacia abajo en el eje Y. Mertens conjeturó en 1897 que el valor de esa función «probablemente siempre sería menor que la raíz cuadrada del número cuestión», lo cual parecía bastante razonable. De hecho se puede calcular para 10.000, 1.000.000, 1.000.000.000 y mucho más allá y siempre es cierta.
Pero resulta que no: en 1985 dos matemáticos, Riele y Odlyzko, demostraron que la conjetura de Mertens deja de ser cierta más o menos a partir de 101064, cifra que luego de algunos refinamientos se redujo a 101040 como cuentan en el vídeo. Vamos a ponerlo en grande para que se entienda mejor y más claramente:
Es un valor tan enormemente grande que es imposible de calcular con exactitud cuál es. Es simplemente un punto límite aproximado a partir de cual se sabe que no se cumple la conjetura, aunque no se sabe exactamente cuándo. De hecho está conectado con la famosa hipótesis de Riemann: si la conjetura de Mertens hubiera resultado ser cierta (que no lo es) hubiera supuesto por extensión confirmar la de Riemann, que a día de hoy sigue sin estar confirmada. Así que habrá que esperar a otra ocasión… o a otro siglo.
Relacionado:
