Por @Alvy — 14 de agosto de 2010
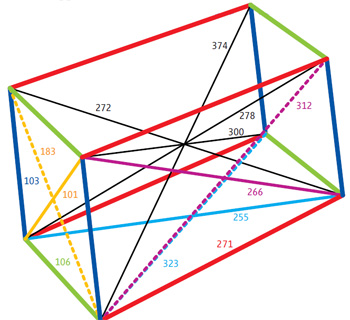
Todas sus aristas y diagonales son números enteros. Tal y como explican en Francis (th)E mule Science's News hasta el año pasado no se conocía ningún ejemplo en que los trece valores de las aristas y diagonales de un paralelepípedo fueran números enteros: los matemáticos pensaban que tal vez ni siquiera existían. Pero mira.
Ahora se buscan cuboides perfectos: paralelepípedos en los que las cuatro diagonales interiores son iguales y donde tanto aristas como diagonales son también números enteros.
