Por @Alvy —
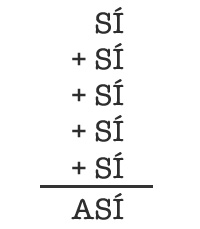
Hay que reemplazar cada letra por una cifra diferente, y no se pueden usar ni el cero ni el uno. El resultado ha de ser la suma correcta tal y como está planteada.
Este problema lo publicó Fermín Pérez en la revista Cacumen #2.
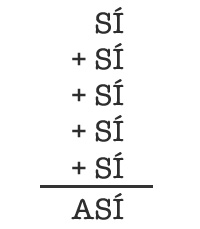
Hay que reemplazar cada letra por una cifra diferente, y no se pueden usar ni el cero ni el uno. El resultado ha de ser la suma correcta tal y como está planteada.
Este problema lo publicó Fermín Pérez en la revista Cacumen #2.
Lo más visto recientemente