En probabilidad, el Teorema del límite central viene a decir que
En condiciones muy generales, si Sn es la suma de n variables aleatorias independientes, entonces la función de distribución de Sn «se aproxima bien» a una distribución normal (también llamada distribución gaussiana, curva de Gauss o campana de Gauss).
En Central Limit Theorem Visualized in D3, una versión animada creada por Victor Powell (inspirada en The Bean Counter) puede verse este efecto en acción, lo cual es mucho más fácil e intuitivo de entender.
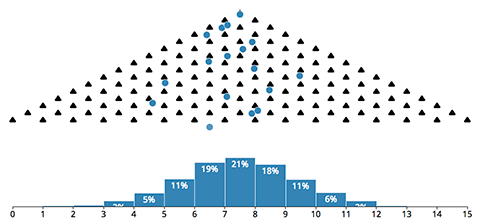
Al igual que en los montajes que hay en los museos de ciencia con clavos y canicas, basta con ponerlo en marcha para deleitarse viendo cómo se va formando la distribución normal a medida que las bolitas van cayendo aleatoriamente, siendo desviadas en cada punto a un lado o al otro según una probabilidad del 50%.
Como hay más recorridos o formas (combinaciones) de que una bolita dada caiga en los intervalos centrales que en los de los extremos, el porcentaje de bolitas acumuladas acaba a la larga siendo mayor ahí.
Con las opciones del menú de arriba se puede variar la velocidad y el número de intervalos para comprobar el efecto de forma más rápida o con más detalle.
(Vía FlowingData.)
Actualización (9 de octubre de 2020) – La web original desapareció, pero la versión que quedó guardada en Archive.org funciona estupendamente, aunque resulta un poco lenta al cargar.