Vi pasar por Twitter esta igualdad, que a simple vista resulta un tanto peculiar e incluso sorprendente:
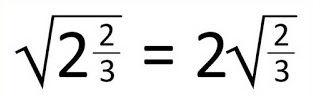
Con la calculadora se puede comprobar que efectivamente sqrt(2+2/3) = 1,6329… y 2*sqrt(2/3) = 1,6329… (Ojo: el primer valor es una fracción mixta).
Es un ejemplo de lo que Pat Ballew, profesor de matemáticas retirado, llama surds, palabra que proviene de un juego de palabras en inglés relativo a las raices cuadradas y el «absurdo» de lo que podríamos llamar «cálculos equivocados y absurdos, pero correctos» que alguna vez se muestran a modo de humor matemático. En estos absurdos prácticamente «todo vale», como en los clásicos:
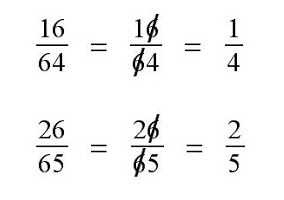
En los que pese a todo, la igualdad sigue siendo correcta (!)
Según explica Ballew el ejemplo de la raíz cuadrada se puede «generalizar» para asombrar al personal con valores mucho más grandes:
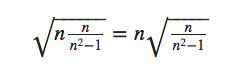
Lo cual si se hace con cuidado y «números redondos» queda mucho más simpático.
Como bonus, otros dos clásicazos de esta temática:
Abbott y Costello en una demostración práctica de cómo 7 por 13 = 28 y –cómo no olvidarlos– Fofó y Miliki explicando la tabla de multiplicar del 9.
Relacionado:



