Por @Alvy — 13 de Agosto de 2011
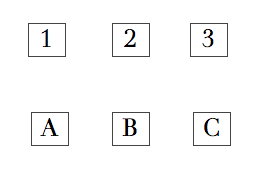
Como bonus al problema de ayer, una mención clásico problema de las tres casas y los tres servicios básicos. Tenemos tres casas A B y C a las que hay que conectar los servicios básicos de Agua, Gas y Electricidad (1 2 y 3). El esquema puede verse en este gráfico.
¿Se pueden dibujar las nueve líneas de conexión
sin que se crucen unas con otras?
Las casas están sobre una superficie plana (o esférica, como la Tierra) y no valen las soluciones 3-D que harían de la solución algo obvio. Como dicen en la Wikipedia, «es un problema abstracto, no de ingeniería».
