Qué mejor que un vídeo de Numberphile en este caso con el profesor David Eisenbud para repasar la famosa Conjetura de Goldbach que viene a decir que
Todo número par mayor que 2 puede escribirse como suma de dos números primos.
Tan fácil de entender. Tan aparentemente simple. Tan profundamente maléfica.
Desde que Goldbach enunció esta conjetura en una carta al mismísimo Euler en 1742 nadie ha podido demostrar que sea matemáticamente cierta – a pesar de que el propio Goldbach decía estar seguro de que lo era… pero había sido incapaz de dar con la prueba. Euler tampoco pudo.
El vídeo explica cómo es muy fácil entender el problema o, más bien, a la inversa: generar un método que proporcione todos los números pares a partir de la suma de dos números primos. También es interesante porque explica cómo se calcula cuántos números primos hay hasta cierto número dado y otras propiedades de estos números que resultan útiles en teoría de números.
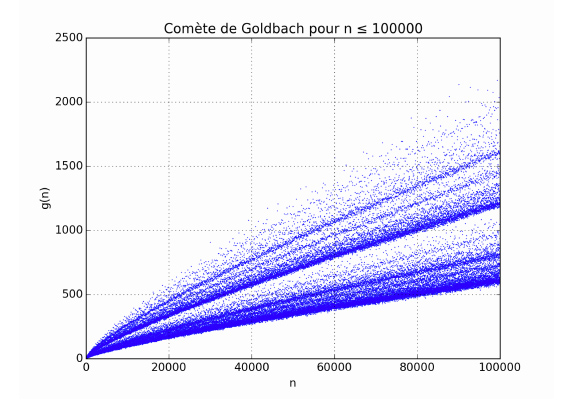
El «Cometa de Goldbach» muestra el número de diferentes formas g(n) en que puede descomponerse como suma de dos primos un número n. Crece y crece… pero no es una demostración / Maths-Algo.fr
En este caso la dificultad del problema parece estribar en que hay demasiadas formas de combinar los números primos, de modo que a medida que se va subiendo en la lista –y se ha comprobado hasta 4 trillones– al final siempre acaba apareciendo una solución válida. Pero que haya muchos casos no es una demostración en toda regla. ¿Habrá algún número, por grande que sea, para el que no se cumpla la conjetura?
Ni matemáticos de la talla de G. H. Hardy, Alan Turing o el mismísimo Ramanujan pudieron con la conjetura de Goldbach – por no hablar de hallar un contraejemplo. Así que aunque ha habido avances a lo largo de los tiempos, ciertas aproximaciones, en su versión más pura se sigue considerando uno de los más bellos problemas de las matemáticas. Fama eterna asegurada para quien consiga dar con la demostración en cuestión.
Relacionado:
- El tío Petros y la conjetura de Goldbach, un libro al respecto



