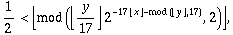Esta es la peculiar Fórmula autorreferente de Tupper:
Es una fórmula bastante curiosa en la que los semi-corchetes gigantes indican la función «redondear hacia abajo» y mod es el módulo (resto) de una división de un número en cierta base (en esta fórmula, base 2).
Lo interesante de la fórmula autorreferente de Tupper sucede al «plotear» (dibujar) la función para los valores de x entre 0 y 105 para valores de y entre n y n+16, siendo n este gigantesco número 543 cifras:
960939379918958884971672962127852754715004339660129306651505519271702802395266424689642842174350718121267153782770623355993237280874144307891325963941337723487857735749823926629715517173716995165232890538221612403238855866184013235585136048828693337902491454229288667081096184496091705183454067827731551705405381627380967602565625016981482083418783163849115590225610003652351370343874461848378737238198224849863465033159410054974700593138339226497249461751545728366702369745461014655997933798537483143786841806593422227898388722980000748404719
El resultado al utilizar ese número cuidadosamente seleccionado es, sorprendentemente… un dibujo de la propia fórmula:
Lo que llamaríamos una fórmula autorreferente. Al más puro estilo Gödel, Escher, Bach.
El secreto para quien le interese: las 543 cifras decimales del número n permiten codificar unos 1.810 bits de información binaria (a razón de unos diez bits cada tres dígitos decimales, más o menos).
El «mosaico» donde aparece mágicamente el resultado de la fórmula tiene una superficie de unos 106×17 bits = 1.802 bits, un poco menos. De modo que toda esa información binaria «cabe» en un número decimal que convenientemente «dividido» (véanse las divisiones y módulos 17 en un par de lugares de la fórmula original) dibujan fielmente bit a bit el resultado original.
Más info en la Wikipedia: Jeff Tupper Self-Referential Formula.