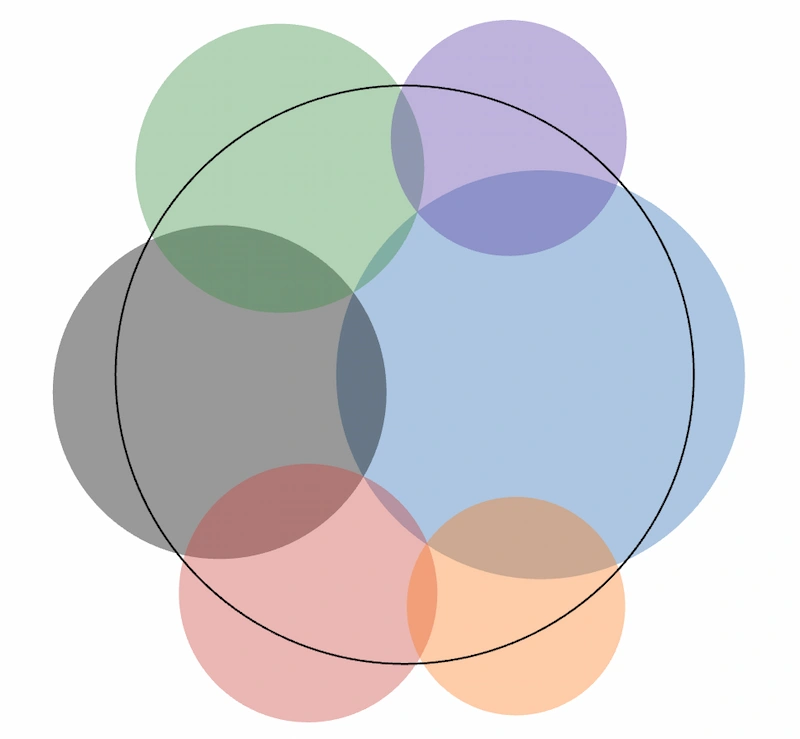
¿Pueden seis círculos abarcar uno más grande en su totalidad? Este curioso problema parece tener solución, aunque si se intenta según se plantea en el enunciado, no es tan fácil.
El problema consiste en cubrir un círculo de área unidad con círculos de áreas 1/2, 1/3, 1/4, 1/5, 1/6 y 1/7, que se pueden solapar. La ordenación más obvia muestra que la cosa no es tan fácil; aunque casi, casi se cubre en su totalidad, quedan algunas zonas con pequeños huecos apenas visibles que hacen que el valor exacto de círculo cubierto sea sólo el 99,96%.
Junto al problema, que apareció en la sección de matemáticas de Stack Exchange, hay un enlace en Desmos, una interesante herramienta gráfica matemática donde se puede jugar con los parámetros moviéndolos con el ratón, en este caso las posiciones exactas de los círculos. Aunque como demostración, demostración, se necesita hacer cálculos.