Visita a Tycho / Andrew McCarthy

El astrofotógrafo Andrew McCarthy pudo realizar hace unos años esta espectacular captura de un tránsito de la Estación Espacial Internacional frente a la Luna [zoom para más detalle] que, como resulta aparente, da para póster y como tal vende en su tienda web a diversos tamaños, calidades, con marco, sin marco, etcétera.

Lo interesante de la foto es que la Estación Espacial parece estar orbitando la Luna, allá a lo lejos, muy a lo Interestelar… cuando en realidad la Luna está a unos 384.000 km mientras que la Estación Espacial está a tan solo 420 km de altitud. El tamaño de la foto completa cubre unos 45 segundos de arco, que es realmente una mínima fracción vista desde aquí pero que hace mucho efecto con las distancias. Es todo un efecto óptico.

¿Cómo se toman estas fotos? McCarthy utiliza Transit Finder, una aplicación que te dice dónde está (y estará) la Estación Espacial en cada momento. Con eso puedes calcular cómo se verá, si merece la pena conducir un poco para pillar el tránsito, etcétera. Luego usa un teleobjetivo de 800 mm aunque uno de 350 mm puede también servir.

Como sabrá cualquiera que haya visto pasar la EEI por la noche, va toda leche. Así que el tránsito frente a la Luna dura menos de 1 segundo. El truco es tenerlo todo preparado con horas de antelación: trípode, posición exacta a la que apuntar, asegurarse con Time.gov de la hora exacta, etcétera. Entonces se lanza una ráfaga de disparos de 1/1000s y a ver si se da bien.

Felicidades por esta toma, que no es la única que ha conseguido, y muchos agradecimientos por la pequeña guía de una página que ha dejado con consejos de cómo hacer este tipo de fotos.

Relacionado:

• Astrofotografía más fácil, cómoda, portátil y con bonitos resultados
• Un preciosa foto de la Luna a 174 megapíxeles capturada en 200.000 fotografías por dos aficionados a la astrofotografía trabajando en equipo
• Na procura da noite: un libro de astrofotografía para disfrutar
• Trazos de estrellas, una iniciación fácil a la fotografía astronómica
• El eclipse solar anular de octubre de 2023 fotografiado en 8K
• Turismo estelar: astroturismo y alojamientos con vistas a las estrellas
• Los timelapses astronómicos de Daniel López

Las nuevas notificaciones y tarjetas en acción

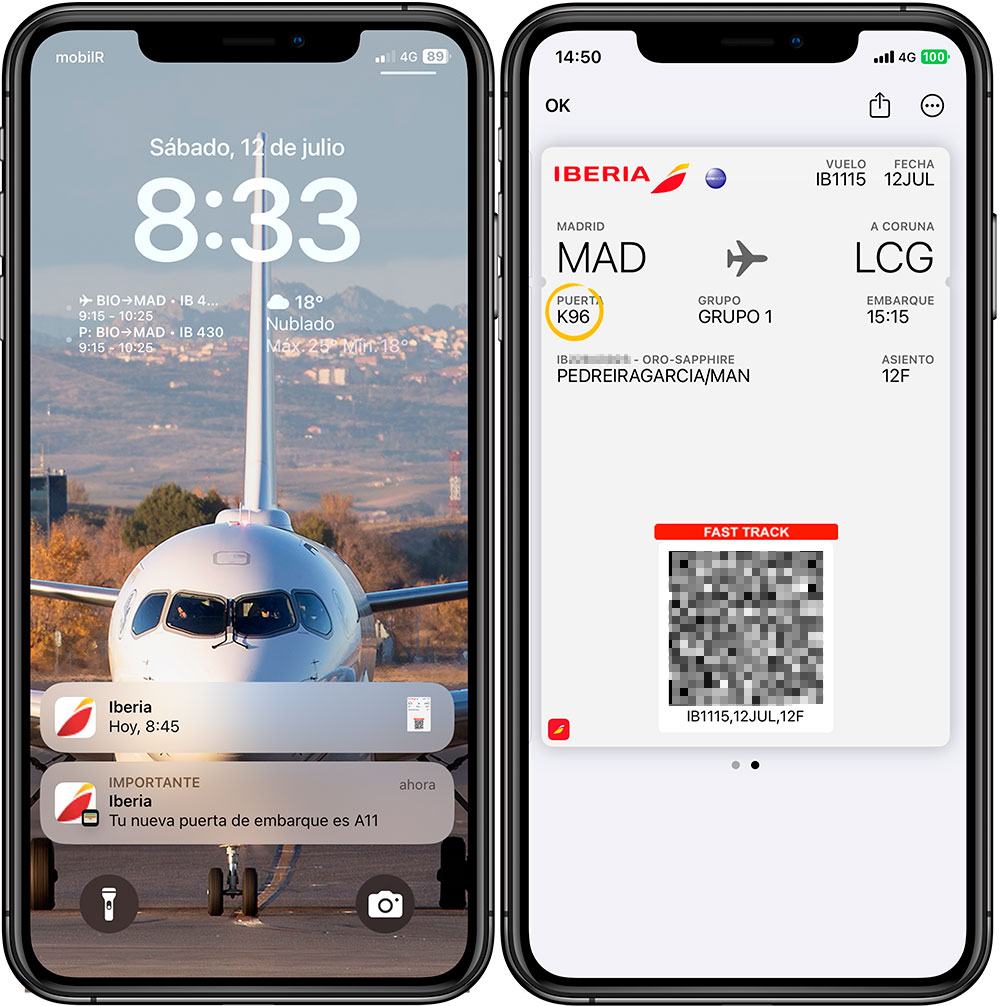
Hace unos días recibí una nota de prensa de Iberia que anunciaba que las tarjetas de embarque en el móvil pasaban a actualizarse en tiempo real con detalles como la puerta de embarque en el momento en el que esta es asignada. O con cambios de asiento o cabina si es el caso. También, si le das permiso a la app de Iberia, recibirás notificaciones con esas actualizaciones. Esta nueva función está disponible tanto para Android como iOS.

Como me tocaba volar unos días después de recibirla estuve atento a ver cómo iba el asunto.

Mi viaje eran dos vuelos de ida y dos de vuelta. Y ya tenía las tarjetas de embarque descargadas antes de que Iberia sacara esta actualización. Así que a la ida, como yo sospechaba, ni notificaciones ni nada. Pero para la vuelta me descargué la versión más reciente de la app para iOS, que en el momento de escribir esta anotación es la 14.21, y con ella me descargué de nuevo las tarjetas de embarque de los dos tramos de vuelta.

Y con eso pude acceder a las actualizaciones en tiempo real, tanto mediante notificaciones, lo que se puede ver en la imagen de arriba a la izquierda, como en las tarjetas de embarque propiamente dichas, lo que se ve en la imagen de la derecha. Las tarjetas, por cierto, muestran la información que se ha actualizado en un círculo amarillo la primera vez que las abres tras haber sido actualizadas para que no tengas dudas de cuál es la información nueva.

Aunque también puedes acceder a esta nueva funcionalidad sin tener la app instalada siempre que te descargues las tarjetas a través de la web de Iberia en formato Google Wallet o Passbook.

Es cierto que esa información ya te llegaba antes por correo electrónico, SMS o WhatsApp. Y a partir de ahora seguirá llegando por correo electrónico. Pero eso suponiendo que Iberia tuviera tus datos de contacto. Porque en el caso de un billete que te hayan comprado no es raro que no los tenga, según lo hábil que haya sido la persona que ha hecho la reserva con esas cosas. Así que lo de las tarjetas que se actualizan ellas solitas es especialmente útil en esos casos.

Pero en cualquier caso esto de las actualizaciones es una comodidad, en especial durante el viaje y para las puertas de embarque, ya que te evitas estar pendiente de pantallas en el aeropuerto. Alguna ventaja tenía que tener vivir en el siglo XXI.

Livesuit. Por James S. A. Corey. Orbit (1 de octubre de 2024).

Esta es una historia corta situada en el universo de La guerra de los cautivos. Pero no sale en ella ninguno de los personajes de La piedad de los dioses salvo los carryx como el enemigo implacable con el que lucha la humanidad. Pero otra rama de la humanidad. De hecho no sabemos si la historia tiene lugar antes o después de lo que cuentan en la novela.

El relato cuenta la historia de Kirin, quien siguiendo los pasos de su amigo Piotr se une a las fuerzas armadas para luchar contra los carryx. Que, ojo, tan siquiera son mencionados por ese nombre en ningún momento. Los dos toman esa decisión como una extensión casi lógica de su trabajo como miembros de un equipo de rescate en su mundo; quieren evitar el sufrimiento de otras personas en la medida de lo posible.

Y solicitan unirse al cuerpo de los Livesuits del título, los trajes vivientes, que son una especie de exoesqueleto dentro del que tendrán que vivir en todo momento durante los cinco años de tiempo real que durará su servicio. El traje les dará más fuerza y resistencia, así como protección contra daños, y poderes casi sobrehumanos. Ellos serán el cerebro del traje.

Entre la distorsión temporal que implican los viajes de un lado a otro y la férrea disciplina militar y control que ejercen los mandos me ha recordado tanto a La guerra interminable como a Starship Troopers. Y he de decir que me ha gustado casi más que La piedad de los dioses.

Aunque también he de decir que el descubrimiento que hace Kirin al final me parece un poco inverosímil. No lo que descubre sino que pueda hacerlo.

Pero en cualquier caso es una dosis de este nuevo universo de James S. A. Corey mientras no llega la segunda novela. Así tendrás tiempo a releer ambos a ver si eres capaz de decidir si la acción de Livesuit tiene lugar antes o después de la de la novela.

_____
El enlace a Amazon lleva nuestro código de asociado, así que si compras el libro o alguna cosa más tras seguirlo es posible que obtengamos algo en forma de comisión.

Acaba de morir a los 89 años Alan Pollack, el piloto de la RAF que pasó a través del Tower Bridge con un avión a reacción. En concreto con un Hawker Hunter. Creía que ya había contado su historia aquí, pero veo que no.

En 1968 la RAF cumplía 50 años. Pero el gobierno del Reino Unido no mostró interés ninguno en conmemorarlo. De hecho estaba dispuesto a aplicar duros recortes al pensar que la fuerza aérea era algo del pasado cuya tarea sería realizada en el futuro por misiles.

Esto tenía muy mosqueado a Pollack. Pero la gota que colmó el vaso fue cuando el cuatro de abril lo enviaron junto con otros tres pilotos de su escuadrón a hacer una exhibición de vuelo a la base de Tangmere. Tras aterrizar después de ella descubrió que nadie sabía que ese vuelo había sido uno de los pocos actos en conmemoración del aniversario.

Así que al día siguiente, cuando tocaba volver a su base, fingió haber perdido contacto con el resto de la formación y tener problemas de radio y se dirigió a Londres. Hizo varias pasadas a bajo nivel pero con el motor a tope frente a las Casas del Parlamento en las que, por casualidad, aquel día se discutía sobre la regulación del ruido de los aviones.

Aunque no contento con ello, y aplicando aquello de from lost to the river, decidió pasar a través del Tower Bridge. Fue una ida de olla considerable. Pero también hay que tener en cuenta que los pilotos de los Hunter estaban entrenados para vuelos a muy baja altura, así que en realidad Pollack debía estar pensando en ponerse una máscara de oxígeno de lo alto que iba.

Airfix sacó en 2023 una reedición de su modelo a escala 1:48 del Hawker Hunter FGA.9/FR.10/GA.11 que, entre otras, incluye las calcas necesarias para recrear el avión de Pollack – Airfix

Al aterrizar fue detenido. Pero en lugar de ser sometido a una corte marcial la RAF lo dio de baja por motivos médicos. Quizás preocupados por su salud mental. A saber por qué.

Pollack no consiguió, como era de suponer, que el gobierno cambiara de opinión. Pero recibió cientos de cartas de apoyo del público, de sus compañeros de la RAF e incluso un barril de cerveza de la compañía aérea British Overseas Airways Corporation, la predecesora de British Airways. Una vez terminada su carrera en la RAF trabajó para varias empresas de defensa y siguió siendo un devoto miembro de la RAF Historical Society.

Cuando sí hubo las correspondientes celebraciones fue para conmemorar el centenario de la RAF, que culminaron con un sobrevuelo de Londres por parte de casi cien aviones en activo e históricos del cuerpo:

Pero fue un sobrevuelo a una altura razonable. Que se sepa hasta hoy Pollack ha sido el único piloto en atravesar el Tower Bridge en un reactor.