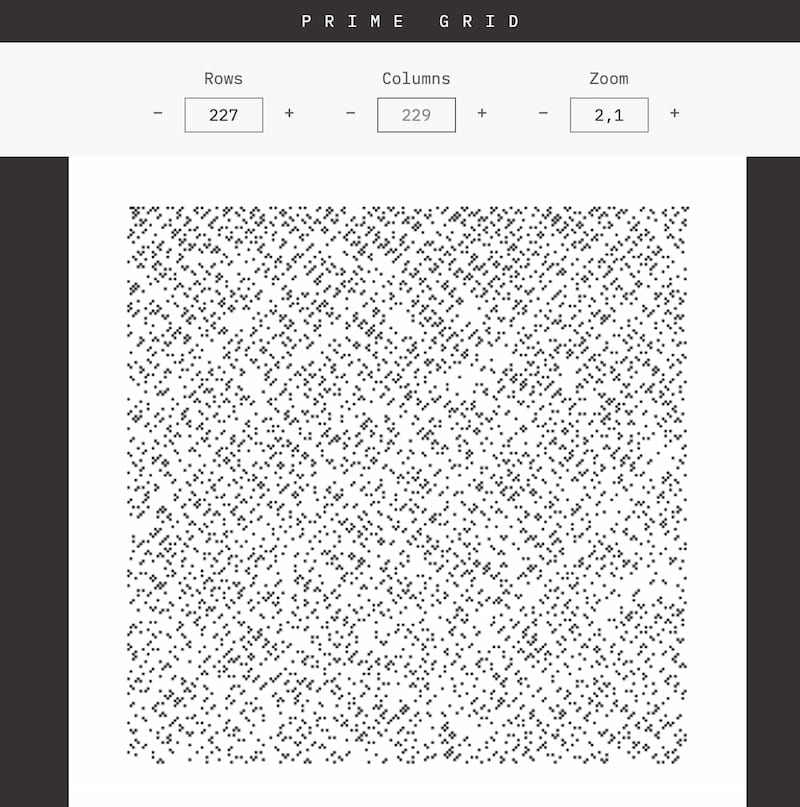
En esta cuadrícula de números primos los números naturales que no son divisibles nada más que por sí mismos y por la unidad están dispuestos en el orden de lectura: de izquierda a derecha y de arriba abajo. Los primos se marcan con un píxel, los compuestos se dejan en blanco. El zoom ayuda a verlo todo al tamaño ideal.

¿Sirve esto para algo? En palabras de Danny Duplex, que se dedica a «resolver los problemas menos importantes del mundo» tan solo sirve para encontrar patrones visuales interesantes, para lo cual se puede variar el tamaño de la cuadrícula, ancho y alto. Como si eso sirviera para algo… Mmm…

Quién sabe si alguien encontrará la respuesta al sentido de la vida, el universo y todo lo demás, o no, pero curioso resulta en cualquier caso. Mi recomendación es intentar entender el porqué de las diagonales y zonas en blanco que resultan tan llamativas; se aprende algo con ello.

También se puede comenzar por un ancho de 2 (donde todos los primos aparecen a la izquierda y sólo el 2 a la derecha) e ir subiendo: esto mostrará la secuencia de los múltiplos de 2, 3, 4, 5… y es también interesante. A veces es meticulosa, a veces es más caótica, con anchos que en ocasiones producen algo que parece código Morse (!) Lo dicho, que cosas más raras pueden llegarse a ver, pareidólicamente hablando.

Tenía guardado por ahí este viejísimo enlace a un artículo del Washington Post donde se explica la estrategia ideal para calcular cual es el mejor momento para dejarse de ligues/novias/novios y sentar la cabeza.

Resulta que el dato es más o menos el mismo que en el problema de la secretaria, aunque con una vuelta de tuerca. En el original, que data de 1949, el problema es tratar de contratar a la mejor secretaria de entre 100 candidatas, pero:

(…) Solo podemos entrevistar a cada persona una vez. Después de cada entrevista, hay que decidir si la contratamos o no. Si decidimos que no, perdemos la oportunidad para siempre. Si entrevistamos a 99 sin haber elegido, tenemos que contratar a la número 100. ¿Cuál es la mejor estrategia?

Aunque puede parecer que la probabilidad es muy baja (1%) en realidad se puede mejorar esa probabilidad haciendo lo siguiente: se entrevista a las 50 primeras –asignándoles una calificación– y luego se elige a la primera que está por encima de la mejor de las anteriores. Gilbert y Mosteller demostraron que con esta idea se podía afinar aun más, llegando al valor casi «mágico» de 37: entrevistar 37 y luego elegir a la mejor. El 100 proviene del valor 100/e (2,7182…)

Pero… ¡quietosparaos! Volviendo al asunto original, el problema está claro que es más complicado: ¿y cómo saber cuántas «candidatas» hay o va a haber a lo largo de tu vida? Ese dato no se facilita, de modo que hay que aplicar un poco de estadística, que dependerá de cada persona en particular: lo selectiva que sea, lo que considere «candidatas serias», el tiempo que quiera emplear en la tarea… Habrá quien tenga tres «candidatas serias» en su vida y quien tenga 30 o 300.

En la práctica, suponiendo un valor promedio de 11 –por ejemplo, como hacen en el artículo– significaría dejar pasar a las primeras 4 personas (primer 37%) y luego elegir a la siguiente que supere a cualquiera de esas cuatro primeras. ¡Problema resuelto! Tal vez no sea absolutamente la mejor elección, pero sí es más probable que lo sea a que se hubiera elegido al azar. (De una probabilidad de ~9 % se pasa a un ~37%).

Al igual que en el problema de la secretaria, este problema forma parte de la teoría matemática de la decisión, que estudia cómo se comportan y funcionan las condiciones y decisiones que tomamos en nuestro día a día.

(Vía When to stop dating and settle down, according to math, por Ana Swanson en el Washington Post.)

Buscando algo de orden en el universo, Gottfried Leibniz publicó en 1666 su Disertación acerca del arte combinatorio, que aunque él mismo más tarde reconoció que no era gran cosa, tiene su interés.

En esta tesis plantea que todos los razonamientos que el ser humano pueda llegar a hacer se reducen a combinaciones de ideas básicas en forma de sonidos, letras o números. Su idea era enumerarlos: planteó una especie de «alfabeto del pensamiento» con los conceptos primarios. Luego se podría jugar con todos los símbolos que lo componían, incluyendo sujetos y predicados, para generar juicios y descubrir verdades. Introdujo conceptos como las permutaciones y combinaciones matemáticas para ello.

Esto sería una forma de razonamiento sistemático en lugar de intuitivo, apto para ser mecanizado. Estaba inspirado a partir del Ars Magna Generalis de Ramón Llull (del 1305, siglo XIV) y, como era costumbre en aquellos tiempos, estos trabajos mezclaban cuestiones matemáticas, lógicas y teológicas, campos a veces no muy desarrollados que hoy en día se consideraría que ni venían a cuento.

De ahí a la Biblioteca de Babel de Borges hay un paso.

Relacionado:

• La biblioteca de Babel de Borges versión Internet
• La biblioteca de Babel como juego 3D
• El tamaño de la biblioteca de Babel
• «La loca idea de una máquina que sepa pensar»

La metamatemática es el estudio de las matemáticas usando herramientas matemáticas, pero «desde fuera del sistema». También estudia la teoría lógica formal de las demostraciones matemáticas. Si alguien hizo famosa la metamatemática fue Kurt Gödel –quién más apropiado– que, entre otras cosas, desarrolló los teoremas de incompletitud, a saber:

1. Ninguna teoría matemática formal capaz de describir los números naturales y la aritmética con suficiente expresividad es a la vez consistente y completa.

2. Si el sistema de axiomas en cuestión es consistente, no es posible demostrarlo mediante dichos axiomas. (O, visto de otro modo, si es consistente, no puede demostrar su propia consistencia).

La metamatemática no estudia los objetos matemáticos en sí mismos, sino las teorías que estudian a dichos objetos y sus propiedades. Si todo esto parece un poco lioso es porque está encerrado en un eterno y grácil bucle.