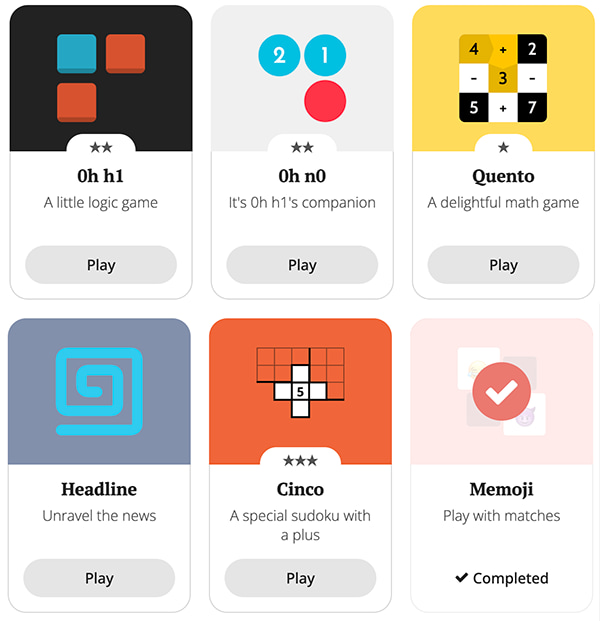
Puzzle Pass es un sitio de pasatiempos lógicos, que tiene algunos originales diseñados por los creadores de la página y otros clásicos que van desde el Sudoku a los crucigramas.
Lo mejor de todo es que son muy estilosos y cómodos de utilizar, con un diseño limpio, una interfaz estupenda y una jugabilidad máxima. En la pantalla siempre hay opciones para ver la ayuda, conseguir algún truco o resetear el juego. Además de eso se mantiene el estado del juego, aunque si quieres probar varios hay que registrarse; con unos clics y una cuenta de Google es suficiente.
Respecto a los juegos en sí, fáciles no son, eso ya lo anticipo. Además muchos tienen el añadido de un reloj de cuenta atrás de modo que no sólo hay que pensar y probar sino además hacerlo antes de que se acabe el tiempo. Requieren paciencia pero a la vez exigen prontitud, una paradoja perversa que sirve para pasar el rato y hacerlo a gusto.
El juego original de los creadores de Puzzle Pass fue 0h h1, al que siguió 0h n0 y luego ya hubo otros. Los hay de números, piezas de colores, letras y palabras, así que por variedad no será.
Relacionado:
- Ocho colores, un juego de lógica relajante
- Slitherlink: un pasatiempo de lógica, números y dibujar líneas
- Pasatiempos lógicos de campeonato
- Hashiwokakero: el puzzle lógico de conectar islas con puentes
- Nonogramas: lógica y números con dibujos como resultado
- ¡Dios mío, está lleno de variantes de Sudokus!
- Encontrar los factores, un pasatiempo estilo tabla de multiplicar
- Retos mentales matemáticos en 30 segundos